University of York
Copyright Notice: This article is Copyright AI Factory Ltd and the authors. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
Background
A previous newsletter article described how AI Factory used Monte Carlo search for their successful implementation of the popular card game Spades. This AI was created using expert knowledge of the game and contains a large number of heuristics developed and tested over many years. Much of the decision making is governed by these heuristics which are used to decide bids, infer what cards other players may hold, predict what cards other players may be likely to play and to decide what card to play.
Monte Carlo Tree Search (MCTS) is a family of game tree search algorithms that have advanced the state-of-the-art in AI for a variety of challenging games, notably for the Chinese board game Go (Browne et al 2012). MCTS has many appealing properties for decision making in games. It is an anytime algorithm that can effectively use whatever computation time is available. It also often performs well without any special knowledge or tuning for a particular game, although knowledge can be injected if desired to improve the AI's strength or modify its playing style. These properties are attractive to a developer of a commercial game, where an AI that is perceived as high quality by players can often be developed with significantly less effort and risk than using purely knowledge-based AI methods. Moreover, MCTS is far less likely to suffer from the tactical blind spots which are almost inevitable when using a knowledge-based approach: MCTS will behave plausibly even in situations that were not anticipated by the AI designer. However this does not come without cost: the AI may indeed avoid many serious blunders, but when an intuitively weak play and a more tactically plausible one actually lead to the same result MCTS might choose either move. If the classical move is clearly superior, but in most situations will arrive at the same outcome, random chance may cause an inferior move to be selected.
Games such as Chess and Go are games of perfect information: the current state of the game is laid out for all to see, and there is no element of randomness in how the game plays out. Much of the focus of AI research to date is on games of perfect information. However many popular games contain elements of imperfect information, whether through randomness (rolling dice, dealing cards from a shuffled deck) or through hidden information (cards held in a player's hand, the "fog of war" in a real-time strategy game).
Our previous work has investigated how to adapt MCTS to games which, like Spades, involve hidden information. This has led to the development of the Information Set Monte Carlo Tree Search (ISMCTS) family of algorithms (Cowling, Powley and Whitehouse 2011). The ISMCTS algorithm is generic and can play any game without the need for heuristic knowledge (although heuristic knowledge is likely to improve playing strength). Additionally ISMCTS has proven to outperform existing techniques for handling imperfect information in tree search. ISMCTS achieves stronger play than knowledge-based AI for the Chinese card game Dou Di Zhu as well as Spades, in both cases without the need for any game specific knowledge This is an exciting new development which provides a strong baseline player in these games and removes the need to integrate extensive knowledge to produce strong play. Knowledge can optionally be included to improve performance and alter the playing style.
This article is a companion to our paper "Integrating Monte Carlo Tree Search with knowledge-based methods to create engaging play in a commercial mobile game" published in the AIIDE 2013 conference. The paper describes how we worked with AI Factory to integrate ISMCTS into their Spades product for Android, and some of the challenges associated with creating an MCTS-based AI that players perceive as strong. This article touches on these issues, but also serves as an introduction to ISMCTS for developers who wish to use it in their own games. We describe the ISMCTS algorithm and discuss its implementation for a simple example game: Knockout Whist. ISMCTS shows great promise as a reusable basis for AI in games with hidden information and potentially removes some of the burden of developing and testing heuristics for complex games of imperfect information. The ISMCTS algorithm is used in the currently available version of AI Factory Spades for the 4- and 5-star AI levels, and AI Factory have already begun using the same code and techniques in products under development.
Information Set MCTS
Many common approaches to AI for games with hidden information use determinization. The idea is to guess the hidden information (for example randomly deal out the unseen cards to the other players), and make a decision based on a representative sample of such guesses (typically tens or hundreds, but sometimes more). Of course the individual guesses are likely to be wrong, but by taking a large number of these guesses, the hope is that we can collect enough information to assess which move is the best on average. One popular technique based on determinization is Perfect Information Monte Carlo (PIMC), which simply treats each determinization as if it were a game of perfect information (e.g. a card game with all cards face up), applies standard AI techniques to each of these games, and uses a majority vote to choose which move to play.
PIMC has proven successful in several games, particularly Contract Bridge (Ginsberg 2001). However, the approach has two serious flaws. First, treating the game as one of perfect information means the AI will not see the value of gathering or hiding information, and will wrongly assume that it can tailor its decisions to the opponent's cards. Second, we have multiplied the amount of work our AI needs to do: each "full" decision is an average over tens or hundreds of determinization decisions, each determinization decision being as difficult as choosing a move in a game of perfect information.
To address these problems, we developed Information Set MCTS (ISMCTS). We keep the powerful idea of randomly guessing the hidden information but instead of treating each of these guesses as an independent game to be analysed, we use each guess to guide a single iteration of MCTS. Instead of growing several search trees and averaging at the end we grow a single tree and essentially average as we go along. For any one determinization, most moves in the tree will be illegal, and the value of a legal move will have been determined from maybe hundreds of positions, none of which coincide with the determinization currently being assessed nor with the actual (unknown) state of the game. This is perhaps a paradoxical way to choose a move, but works through summing large numbers of imprecise assessments to yield a statistically meaningful result.
A full description of how MCTS works is available here; what follows is a brief overview. MCTS builds a portion of the game tree. The decision of which parts of the tree to grow is a trade-off between exploitation of parts of the tree that look promising and exploration of unknown avenues. This focuses the portion of the tree on the most interesting and relevant lines of play, unlike the brute-force approach of alpha-beta search (which considers all of the tree except those that can be mathematically proven to be irrelevant, and usually requires a depth limit to reduce the search tree to a manageable size).
A basic MCTS algorithm has four steps:
- Selection: Starting at the root of the tree, choose a child node according to a multi-armed bandit algorithm (see below). Then select a child of this child, and so on until you reach a node with untried moves.
- Expansion: Add a node corresponding to one of the untried moves, chosen at random.
- Simulation: Starting at the state corresponding to the expanded node, apply random moves until a terminal (end of game) state is reached.
- Backpropagation: According to the simulation result, update the win and visit counters in the newly expanded node and in each node that was visited by selection.
The key to balancing exploitation with exploration is the multi-armed bandit algorithm used in the selection step.
The most common choice is UCB1, which chooses the node with the maximum value of:
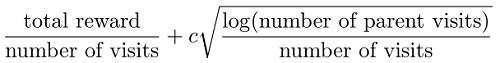
The first term is simply the average reward from all simulations through this node, which takes care of exploitation. The second term is large if the number of visits to the node is small relative to the number of visits to the parent, i.e. if the node is under-explored. The constant c allows the balance between exploitation and exploration to be tuned; if the simulation rewards are between 0 and 1, a value of c = 0.7 usually works well.
ISMCTS works in a very similar way to plain MCTS, with the addition of an extra first step and some other changes:
- Determinization: Randomise the information hidden from the AI player in the root game state.
- Selection: As in plain MCTS, but the child nodes available for selection are restricted to those that are compatible with the determinized state.
- Expansion: Again, the set of untried moves is restricted by the chosen determinization.
- Simulation: Works exactly the same as plain MCTS.
- Backpropagation: Works exactly the same as plain MCTS.
The key thing to note about ISMCTS is that each node in the tree does not correspond to a single state, but to a set of states which are indistinguishable from the AI player's perspective. In game theory such a set is called an information set because it is the set of states where the player sees exactly the same information, i.e. the states only differ in the hidden information (e.g. the opponents' cards in hand for Spades).
The states in an information set may have different available moves. For example in many card games, the moves available depend on the cards in hand. A tree node where an opponent makes a decision needs to have a branch for every move the opponent could possibly play, corresponding to every possible card that opponent may be holding. ISMCTS deals with this by choosing a determinization, and ignoring all moves throughout the tree that are not available for this determinization. This has two benefits: in effect it reduces the branching factor of the tree, and it guarantees that rarely available moves are searched less often than more common ones.
Implementing ISMCTS
The code accompanying this article (ISMCTS.py) is a simple implementation of ISMCTS in Python, playing the card game Knockout Whist. The full rules for Knockout Whist can be found on Pagat. Knockout Whist is similar to Spades in that both are trick-taking card games, but Knockout Whist does not involve bidding or complex scoring rules and hence is simpler to implement.
For a game to be playable by ISMCTS, only one data field and four functions need to be defined:
- playerToMove: The player making a move from this state.
- CloneAndRandomize(observer): Create a copy of the state, then determinize the hidden information from observer's point of view.
- GetMoves(): Get a list of the legal moves from this state, or return an empty list if the state is terminal.
- DoMove(move): Apply the given move to the state, and update playerToMove to specify whose turn is next.
- GetResult(player): If the state is terminal, return 1 if the given player has won or 0 if not. For other games, this function could return 0.5 for a draw, or some other score between 0 and 1 for other outcomes. If the state is not terminal, the result is undefined.
The main implementation of the algorithm is in the ISMCTS function, which calls the methods of the Node class. If the comments and debug output code were removed, the algorithm could be condensed into fewer than 50 lines of code. The UCBSelectChild and GetUntriedMoves methods are particularly important: these use the list of legal moves from the current determinized state to filter the nodes available for selection and expansion respectively.
Implementing ISMCTS efficiently in C++
Many of MCTS's success stories have involved running it on powerful computers, or even in parallel across clusters of machines. Smartphones and tablets are getting more powerful every day but are still a long way off this level of performance, so efficient use of CPU time and memory was a priority for our work with AI Factory. Also, AI Factory work in C++ for several platforms, so we could not rely on the nice data structures and library functions available in Python or even on the C++ STL.
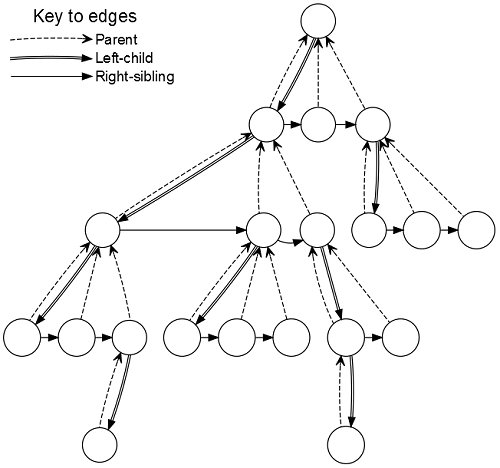
We used a left-child right-sibling representation for the tree. Each node has pointers to three other nodes: its parent, its first child, and its next sibling. The children of a node thus form a singly-linked list. For comparison, a node in our Python implementation stores a reference to its parent and a list of references to its children. This tree representation is illustrated in the following figure:
Instead of creating new nodes as the search progresses and then deleting them afterwards, we allocate one array of fixed size containing all the nodes we will need for the search. Each ISMCTS iteration adds a single new node to the tree, so if the number of iterations is known in advance then the amount of memory needed is also known. During the expansion step we simply take the next unused node from the array, initialise it, and add it to the tree. This allows us to completely avoid the C++ new and delete keywords, along with the associated headaches of memory leaks, unpredictable (potentially high) memory usage, slow performance and memory fragmentation. If the number of iterations is large or variable, we can still work with a fixed memory buffer by adding nodes less frequently than once per iteration, or by deleting less promising regions of the tree and reusing the memory for new regions.
As always when writing efficient code, the golden rule is to profile before optimising. This allowed us to identify the bottlenecks in the parts of the game logic most exercised by ISMCTS (cloning the game state, generating lists of legal moves, playing moves during simulation) and ensure these parts were as efficient as possible. We also obtained some benefit by replacing the expensive logarithm and square root functions in the UCB1 formula with precomputed lookup tables.
How well does ISMCTS play?
To demonstrate the playing strength of ISMCTS, we played a large number of AI-versus-AI games comparing the knowledge-free ISMCTS algorithm to the knowledge-based AI for AI Factory Spades and Dou Di Zhu. In each of these games, both members of a partnership use the same AI. In both games the knowledge-free ISMCTS algorithm achieves a higher win rate than the knowledge-based AI. The ISMCTS player also makes decisions quickly, even on a mobile device: 2500 iterations give a strong level of performance, and take less than a quarter of a second on a modern mid-range handset.
For Dou Di Zhu ISMCTS won 62% of games and for ISMCTS Spades 64% of games. On the surface of it, it may not look too impressive that ISMCTS outperforms the knowledge-based approach by "only" 12–14%. However it is important to note that the knowledge-based players were developed over many months of testing and tweaking, requiring deep strategic insights into the games, whereas the ISMCTS players were developed in a matter of days, and gave strong performance out of the box, with no knowledge other than the game rules.
Adding knowledge
ISMCTS gives objectively strong performance without any game-specific knowledge. However, one of the consequences of its lack of human knowledge is that its play style can sometimes be startlingly un-human. A prime example of this is when all simulations are returning the same result, i.e. when ISMCTS can see the outcome of the game is already determined. A human player would still play somewhat plausible moves in this case, in an effort to safeguard the win or avoid a crushing defeat. ISMCTS however plays completely randomly: if the choice of move has no effect on the outcome, then why prefer one move over another? When AI Factory sent Spades with ISMCTS out to beta testers, we were a little surprised by the feedback: even though the ISMCTS player was objectively stronger than the previous AI, it was perceived as weaker. It only takes a single blunder to tarnish the player's impression of the AI's strength, especially if it is the player's partner who makes that blunder.
To address this problem, we integrated heuristic knowledge into ISMCTS. Full details of how we did this are in our AIIDE paper. Importantly, ISMCTS still has the final say on which move is played: the knowledge merely gives the search an initial nudge in the right direction. Many of the heuristics were repurposed from the existing knowledge-based AI code, but not all of them were needed. If we had had to create this knowledge from scratch, it would still be much easier than creating an entire knowledge-based player: essentially, it is easier to come up with rules for which moves (plural) to avoid than to recommend which move (singular) to play. We can let ISMCTS fill in the gaps.
Our first attempt at adding knowledge appeared to make no measurable difference to ISMCTS's playing strength in our tests; in fact it appeared to make it a percent or two worse. The user perception though was that it was stronger as it played fewer inconsequential bad moves, so gave a better playing experience. Those weak moves may not cause the AI to lose games to any statistically measurable degree, but eliminating them makes the AI appear much smarter. The lesson here is that AI-versus-AI playing strength, the benchmark of choice for AI researchers, is no substitute for play-testing with real humans when it comes to developing AI that acts intelligently. Further refinement to the injected knowledge has further improved player experience, but has also now resulted in a player that is measurably stronger than the plain ISMCTS player.
Conclusion
ISMCTS is a general purpose algorithm for hidden information games which performs well without any knowledge beyond the game rules, and is efficient enough to run on current mobile devices. Developing a strong AI based on MCTS requires less effort and time than developing one built purely on knowledge-based approaches. In addition ISMCTS is automatically adaptive to rule changes that might otherwise require time-consuming and risky heuristic adaptation. This is a substantial boon for a commercial implementation, where there is much pressure for rules variants: e.g. AI Factory Spades supports 1296 different combinations of rules, which ISMCTS automatically absorbs.
The existing knowledge-based AI for Spades was already a market leader, and generally recognised as strong. The MCTS-based player performs better by a statistically significant margin, playing at or above a level for the previous AI which consumed over 8 times as much computation time. The core ISMCTS implementation was designed to be highly generic and reusable, and now constitutes a ready-made AI module that can simply be dropped into future projects to produce a strong level of play with almost no modification. Indeed, AI Factory are already using the same code for new games currently in development. The MCTS framework also provides extensive hooks for game-specific knowledge injection to improve both objective playing strength and subjective playing style.
Although MCTS is objectively strong, play testing revealed that there are some situations in which the decision made by a prototype of the MCTS AI appeared weak to a human player. Integrating the knowledge from an existing knowledge-based player with ISMCTS helped improve the perceived quality of the AI's decisions. As this was further developed by AI Factory the knowledge input made the ISMCTS version significantly stronger. Our upcoming paper at the AIIDE 2013 conference discusses how knowledge can be used to improve the quality of play made by ISMCTS.
This work was funded by grant EP/H049061/1 of the UK Engineering and Physical Sciences Research Council (EPSRC).