Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
Our most absorbing activity right now is the production of puzzles. The major requirement for this activity is to be able to solve these, as this is vital for puzzle creation. Obviously ideas exercised in 2-player game solving, such as Chess and Shogi, are re-cycled but extra twists are added and it is not as easy as it looks.
This article shows how we approached solving our own new puzzle game Move-it ™ and what problems we encountered along the way.
The Puzzle Being Solved
Move-it ™ is a game in the genre of Nobuyuki Yoshigahara's famous Rush Hour puzzle. In this game the player needs to shuffle blocks around on a board so that one particular block can be moved to the other side of the board. This is given physical meaning by linking it to the metaphor of parking cars, where each car can only move in one plane and you have to re-arrange the cars so that the player's "car" can escape.
However there are very significant differences between this and Move-it. In Move-it the shapes can move in any horizontal and vertical direction and come in a variety of shapes, see below:

Here the player needs to move the red square from the bottom left to the top right corner (marked by the red square on the grid). To do this all other shapes must be moved out of the way. This makes for a much broader and challenging puzzle type.
Why is this Difficult?
The puzzle above is relatively easy, but still needs 37 moves to complete. That is the kind of depth of puzzle that is just about within the range of conventional off-the-shelf methods, but would still take a very long time to solve. If you were trying to create new puzzles you would need to test them to see if they can be solved. Using conventional methods it would probably take too long to determine whether the above puzzle could be solved or not.
If we rack up to a more complex puzzle such as this:

This puzzle appears to be more simple but actually needs 72 moves to solve it. Some other puzzles need much more than this, up to 140 moves. At this point, solving using conventional pruned search is very slow and actually a simple full-width minimax search would need to search around 2.0 x 10^34 positions, or 20000 million million million million million million positions.
Of course minimax search can be radically shrunk down using many pruning methods, including the very powerful alpha beta algorithm, which in this case could reduce the tree to about just 3.0 x 10^17 or 30 million million million positions. However there is a catch:
Alpha beta does not help one-side search trees, but instead depends on a 2-player game, where player A can stop player B playing a move because they can prove a better variation elsewhere.
So standard "off-the-shelf" minimax search mechanisms are probably not going to be good enough. We need to dig deeper.
The Plan
So we have to use other methods, and a common approach is forward pruning using heuristics. This may limit the number of moves examined at each branch, but can also stop branches progressing at all. The latter technique is massively powerful as whole sections of the search tree can be eliminated at a stroke.
However to do this requires heuristics as it depends on the tree search examining the position reached, before solving, and then making a decision not to search further. This offers some very clear generic ideas, as follows:
| 1. | Stop the search backtracking or repeating. | |
| This is natural and obvious. It is pointless to move A->B and follow immediately by B->A. This requires no explanation. Further to this: Do not search if you reach a position you encountered before. | ||
| 2. | Track whether the red block has made any reasonable progress. | |
| This can measure how far the red block has moved given the number of moves it has made. | ||
To make (1) above effective you need to also have a hash table, so that you can trap transpositions, i.e. spotting different sequences of moves that reach the same position. Hash tables are a must for almost all tree-searching programs.
Progress, (2) above, is much more problematic. One simple approach might be to simply determine a goal "rate of progress" for the red piece in terms of the average number of moves required to move the target piece just one square.
For this purpose we have a much simpler puzzle to consider, which is shown below in the testbed format so it can be more easily related to the subsequent analysis.
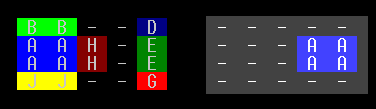
In this position the piece to be moved is blue and marked by the letter "A". The right hand grid shows an empty board with just piece "A", showing the relative position that "A" is trying to reach. In this case, if the board was empty, the puzzle would be solved by just making the 3 moves A-Right, A-Right, A-Right.
This particular position had been hand-solved in 30 moves (it can actually be solved in 27, as found by later version).
Heuristic 1: Measure the number of moves needed to move "A" one square
Using Heuristic 1 actually runs into difficulty very quickly. If you look at the solutions you find that the progress of the square "A" is erratic. In the hand-solved solution "A" does not move at all until 10 other moves have been made, and then it moves twice, followed by a further 8 moves by other pieces, when it moves once, followed by 7 other moves.
This quickly proves to be very inadequate. The search needs to be so tolerance of the "A" piece progress that the pruning then becomes totally ineffective.
Heuristic 2: Also map where the empty squares are
The problem with Heuristic 1 above was that the main piece moving is an infrequent event, and therefore is an inadequate way to measure progress. What is needed is another means of measuring progress that changes frequently. The first obvious candidate is to track where the empty squares are. Clearly it is a good idea if there are less empty squares near the start point and that the squares that "A" must occupy should be empty. The following shows a table of values for the position of "A" and the value of squares.

This is making use of an evaluation principle called hill-climbing, covered in a previous article, where a tree search is allowed to progress from start to a won/solved position by achieving intermediate steps. However there is an important issue here. In a 2-player game such as chess we are most certainly not working out our final checkmate when making our first move, so our hill walk can simply take us to a better place.
In this situation, however, reaching some intermediate point has no value as a final search solution as any such position might not lead to a final solution. We are using this hill walk simply to optimise our tree.
Taking the above evaluation we can examine the evaluation that it gives for each move in the known solution, as follows:

This shows how evaluation changes from move to move. Unfortunately it is not a very smooth transition. For the first 9 moves it looks flat, in which case the evaluation is giving the search nothing. More critically between move 12 through to just one move before solution it takes the evaluation through a dip and eventually returns to the same value.
This is clearly very unhelpful. What we need is an evaluation that gives us a continuous evaluation increase, so that each move in the solution sequence generally delivers some small improvement. Given that, we continuously climb this evaluation hill and easily optimise the tree search. The next section has such an evaluation.
A Smooth Sloping Evaluation Hill: … Bingo! (?)
After some subtle adjustments the evaluation improved so that we had such a slope, as follows:
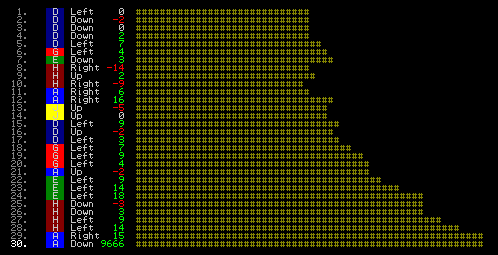
Here we clearly have a pretty consistent slope that helpfully even looks fairly linear near the solution point. It is a bit choppy up until move 12, but that should be enough to allow us to climb an optimised tree all the way to solution.
Of course this evaluation is good for this position. To employ it to optimise the tree we need to use it to prune our branches. However we need to know how much progress is "good" progress. If the Puzzle requires a deep solution, the evaluation climb might be slow. The natural solution to this is to assess the slope on-the-fly. So as we search we record the steepest evaluation slope we can find and use this as a reference target slope to reach. This is a natural self-adjusting mechanism that can be re-applied to all our puzzles. We could prune out branches that are significantly under-performing compared to our most "successful" branch.
What could go wrong?
Unfortunately, quite a lot. When you apply this evaluation and search on it, the program fails to find the solution, even though there seems to be a clear path to take us all the way there. When you examine the moves the search considered favourite, you find the following:

What has happened here is that our evaluation indeed gives us a path to solution but also gives us other, much more attractive paths, to dead-ends. The slope is immediately steeper than our solution slope. Our search gets distracted and weeds out the correct lines because they "under-perform" evaluation-wise compared to the dead-ends. Of course, we can tune this for increased evaluation tolerance, but then the search grinds to a halt.
Making the Evaluation Smarter
To start to address this you need more intelligence in the evaluation, which also makes it slower. Fairly obvious enhancements are to explicitly track the blocking squares in front of the "A" and also to try and occupy squares vacated by "A" moving.
Other things needed are to measure the degree of change. It is easy to thrash pieces around without repeating or actually making progress. The evaluation needs to be able to spot this.
On top of this is the problem that, even with a relatively smart evaluation, many puzzles still require solutions that involve long sequences that would not be found using an evaluation of the type above, so we need more, as follows:
Making the Search Smarter
To get the search to make the next step to solving the above solution, and also much more difficult puzzles, requires a fresh look at searching. The regular minimax toolbox is not enough for this and the search also needs new ideas. Searching to 140 moves deep you need to have other ways of controlling the search complexity and also making sure that the search is able to follow paths that the basic evaluation would not have expected.
This required new techniques, which we have devised for our solver, allowing the search to use probability to find the correct path. Right now this is very much part of our more valuable company intellectual property, so it is too early to discuss it here. However the previous analysis above took us a long way towards solving the problem.
Our current engine solves the 27 move test position above in about 10 seconds. The 72 move puzzle takes about 30 seconds.
This technology is now in use on a wide variety of puzzle types, for both stand-alone puzzle games as well as embedded puzzles for adventure games.
Jeff Rollason - January 2010
