Copyright Notice: All code and ideas expressed in this article are Copyright AI Factory Ltd and the Unbalance corporation.
You may only use these with the direct written permission of AI Factory Ltd.
All of the articles to date in this series have been concerned with either perfect information games, or simulation where most of the data is presented for assessment. In game playing there is a huge genre of games where the key information is deliberately hidden. Of these the most widely familiar game is Poker, where not only is information hidden, but that the core of the gameplay skill is deceiving your opponent about the nature of this hidden information (bluffing). AI Factory also has engines where players conceal information, including Poker, Hearts, Spades and Gin Rummy. This article takes a look at the simplest of these, Gin Rummy, and considers how basic AI can be created to allow hidden information to be assessed.
The Game
I will assume that the reader is familiar with this game, but if not I recommend a quick glance at http://en.wikipedia.org/wiki/Gin_rummy. The basic play is for each player to be dealt 7 cards and take it in turns to either take the turned-up card or new card from the deck, and then discard a card. The object is to have all cards either in sets or runs of at least 3 cards. Scoring is from dead cards remaining in the player's hand at end-of-play, where face cards are penalised by 10 and others by 1. Therefore holding face cards that are not part of a current set is a high risk. A player may "knock" or end a round once they have only 10 or less penalty points in their hand.
The Basis for Making Gameplay Decisions
From above, the primary goal is to reduce the number of penalty points in your hand while maximising the opponent's points. This is a game where you cannot see the cards in your opponent's hand or the cards left in the deck. However there is exposed information available to the player to help assess the play, as follows:
| 1. | The player knows what cards they currently have. | |
| 2. | The player can observe which cards have been exposed in the turn-up and are unavailable. | |
| 3. | The player knows the opponent does not have the player's cards or the cards in (2). |
This may seem meagre information, but a player that uses just the information from (1) will still be able to play a plausible game of Gin Rummy. This would mimic a human player that can completely assess the cards in their hand, but who forgets which cards have already been discarded or picked up by the opponent. From this low base you can concentrate on maximising the combinations of sets and runs possible in your hand, working out that (for example) having 2x 10's is more promising than a 4+6 of hearts, as there are 2 ways of completing 3x 10's, but only one way of obtaining 4,5,6 of hearts. A number of casual players probably play at this kind of level.
Take this one step further and (2) and (3) above can be used to improve the assessment. Now you remember what cards you saw the opponent pick-up, what they discarded and what you have discarded. This allows an improved assessment of probability. For example if you have already discarded a 10, then in the situation above the 2x 10s remaining are no better than the 4 and 6. If both 10s have gone, then your remaining 10s cannot make a set.
An AI player that has such an understanding of (1), (2) and (3) above will actually play quite well. Such an AI player might fail to take any inference from the opponents play, but will have the advantage of completely accurate card counting, which humans are generally not good at.
Raising the bar: Making Inferences from opponent Play
This is the assessment of hidden information. As human players we will naturally make such inferences when playing Gin Rummy. If your opponent discards a 6, we can reasonably assess that they probably do not have another 6, particularly if early on in play. From this we can surmise that whatever 6's we do not already hold may well be in the pick-up deck. Conversely if they pick-up a 6, and we have a 6, then best not to discard it early as they probably want that one too.
A player that makes use of this information can make much better probability estimations about what cards they may well obtain. In this assessment they will not only be maximising their hand but trying to reduce the options for their opponent.
Using Inferred Information to Change Evaluation
Assessment in our Gin Rummy program follows the general model of using a linear evaluation which sums the value of a set or run x the probability that it may happen, and subtracting the same type of value for estimations for the opponent's hand. This naturally credits cards that can be involved in more than one set or run, which anyway improves the chances of obtaining a set or run.
We can look at an example play of a few cards, from the testbed version of our Gin Rummy.
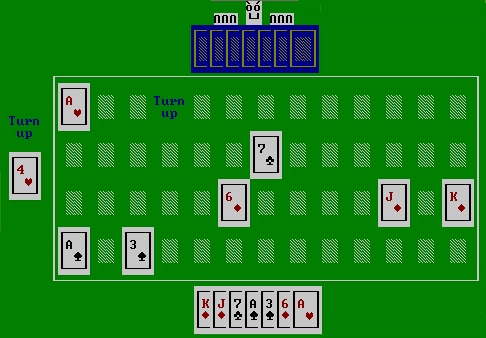
This is the starting position with the human player at the bottom to play. The player's cards are also laid out on the table, ordered by suit, so that it is easy to assess The next plays for both sides are:
| We | pick up 8D from deck and discard 6D | |
| Opp | pick up and discard 6H |
AI opponent can infer from this that we probably do not have any 6's or 5H or 7H (following screen). The AI opponent having picked up a 6H knows that it is not a good card as the 6D has already been discarded.
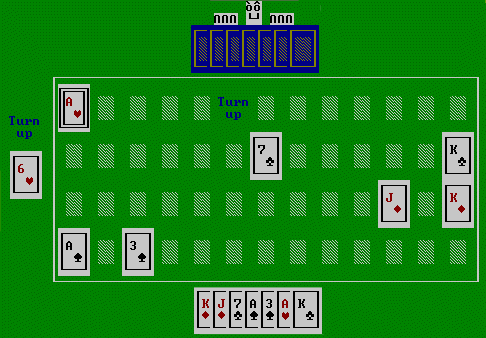
Next:
| We | pick up 10C from deck and discard 7C | |
| Opp | pick up JH and discard 7S |
AI opponent can infer from this that we probably do not have any 7's or 6C or 8C (following screen).
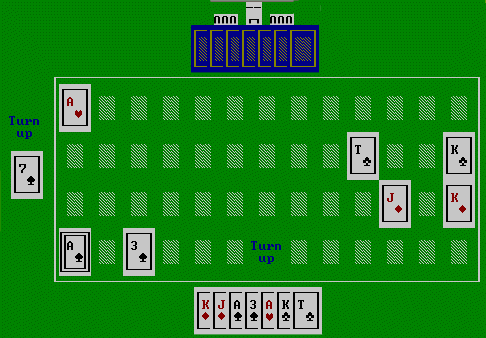
Next:
| We | pick up QD from deck and discard 10C | |
| Opp | pick up 2D and discard 2H |
AI opponent can infer from this that we probably do not have any 10's or 9C or JC (following screen).
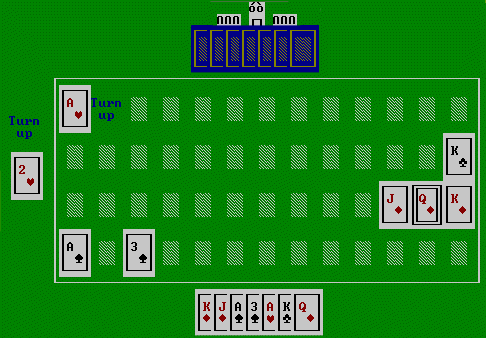
Finally:
| We | pick up 2H from deck and discard KC | |
| Opp | pick up 2D and discard 7H |
This is more information. The AI opponent can infer from this that we probably do have 2's or AH or 3H but do not have K's or QC or JC (following screen).
We can now look at the probability distribution from playing just these 4 cards each. This shows an estimated "relative probability" in the range 0.0 to 1.0 (rounded) for the marked cards. Cards start with the midpoint probability of 0.5, so that it can equally be scaled up and scaled down.
| We | pick up 10C from deck and discard 7C | |
| Opp | pick up JH and discard 7S |
AI opponent can infer from this that we probably do not have any 7's or 6C or 8C (following screen).
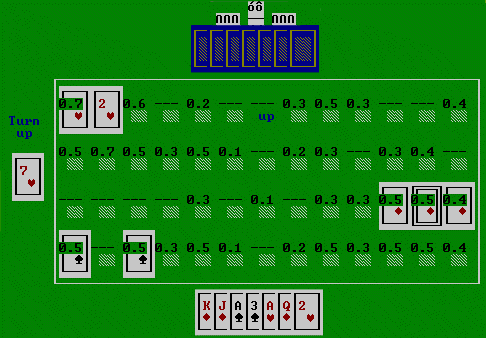
From this you can see that the only card of ours that has a below normal probability is the KD at 0.4. The only elevated probability is the AH. More important is that other cards that we do not have have depressed probabilities. Note that the 2H is unflagged as this is probability 1.0, because the AI saw us pick that card up. If you summarise this:
| Mean probability of cards we do have | 0.52 | |
| Mean probability of cards we do not have | 0.35 |
Considering that only 4 cards have been played then the inference system has picked up quite a bit of information. When this is applied to assessing cards to discard, it has a significant impact. The AI will see that discarding a 3H is bad as we probably have AH (correct) and may have 3C (wrong) and 3S (correct). However discarding 9H is safe as we probably do not have 8H, 10H, 8C, 9S, 9D, which is correct in all cases.
In terms of auto-play this gives the version that can infer possession or absence of cards a win advantage of about 60%.
Conclusion
This is a simple system that can be enhanced to add many further subtleties to make more sophisticated inferences. However the key point is that this simple system proves to be very effective, even with so little data. The system above can be used to provide a capable AI player just using the fast linear evaluation used above. This is very fast and works well.
However if you use this to drive an evaluation based on Monte-Carlo searching, then it becomes a highly effective way to direct search to consider probable branches in preference to unlikely ones. This would allow a much more accurate assessment of a play. We are working on this in Poker and will be using such techniques in other Monte-Carlo and UCT type games.
Jeff Rollason: September 2007
