Copyright Notice: All code and ideas expressed in this article are, by default, Copyright AI Factory Ltd. You may use these, only with the direct written permission of AI Factory Ltd.

This follows work completed for the Unbalance Corporation for creating a highly realistic Aquarium for running on a mobile phone. Such emulations do already exist in other products, but these are generally relatively primitive. The goal here was to create something that both looks like, and behaves like, a real Aquarium.
The article considers some of the issues in creating such a product. This first part deals with the representation of the fish and animation control.
The Project Plan
This is not the kind of product where you can start right away churning out the game primitives. An essential first stage here was to analyse real fish behaviour in depth and to try and devise a framework that could be used to emulate it. For a start we were not going to have infinite processor resources to model this (as the target platform was a mobile phone), so it needed to be capable of being run on a very limited system.
A key here was visiting Aquariums and (with permission), taking fish movies. These were analysed to classify the range of behaviours associated with fish. Superficially, this might sound trivial. Fish do not have legs, cannot climb trees and generally do not do much. However that is deceptive: fish have the freedom to move in any direction, and are not limited to navigating a 2D surface, which is where most animals spend much of their time. They also can move pretty well in any direction from a standing position. They do not just progress like darts, moving forwards. They can rotate their body in multiple planes, while moving in any X,Y,Z direction. No - fish behaviour may appear limited, but can actually be highly complex.
A major advantage, of course, is that the range of body deformations of a
fish is obviously limited, so this limits the complexity for manipulating
any models created. Very quickly the initial plan fell into place, as follows:
Mapping Behaviour to a Single Generic Scheme
One thing was for sure: given that this needed to be developed in reasonable time and on a limited system, it was necessary to find that single core scheme that could be shared by all fish. A consideration here is the handling of animation. If we attempted to have the fish AI have direct control to deform any fish model to show the current fish state, then we would be inviting serious trouble. Such a process would make tuning extremely hard, as the interface for the AI to deform the models would be very complex. The only practical solution is to use a set of pre-defined animations for each fish, that represented all the major states that a fish could be in, but was common to all fish. This has the added substantial benefit that an animation can be developed completely outside the AI framework, using pure modelling tools, so could be independently carefully crafted to match the real thing.
On a simplistic level this can be reduced to just the following:
Swim fast
“Drift” may sound trivial, but actually a fish not actively swimming is not quite like a floating rock, so is going to need some animation. Also it might seem imaginable that Shallow turn is just a subset of Sharp turn, but that is not the case. The motion that flexes for shallow turns may require a different flexing motion. Also trying to stop an animation early and winding back only works if the motion is symmetrical. Simply playing part of the sharp animation to give a shallow turn does not work.
These animations need to be linked up, so that fish can seamlessly switch from one animation to the next.
Linking up Animations
Taking the start of “Drift” as some central common shared point, the emulator could start other animations from this one common point. For example “Drift” could start a “Sharp Left” animation, which eventually ends in a common Drift state. This looks like it could be applied to swim motion too, where the neutral “Drift” corresponds to a neutral stage in the swim motion. However attractive this might seem, unfortunately this requires that a phase during swimming will coincide with the neutral Drift state. If you examine the actual swim animation implemented below (25% shown):

Here you can see that no part of the animation is going to correspond to neutral Drift. The very last frame here is clearly going to be followed by the tip of the tail dragging to the right while the mid section of the tail moves to the left. To fix the animation to have a neutral stage in the swim motion will result in a fish that swims like one of those wind-up toy fish that you can play with in your bath (.. as indeed one of our Aquarium rivals does!).
With this simplification ruled out, the alternative is to have additional linking animations to the swim animations. This is hard to visualise, so is summarised in the diagram below:
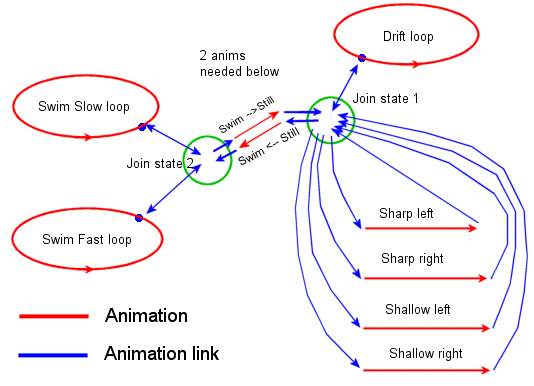
From this, if a fish is executing a turn, but wants to swim, then it needs to do the following:
| 1. | Finish the current turn animation, leaving the animation at “Join State 1” | |
| 2. | Start a “Still to Swim” animation to reach a common point in a Swim animation | |
| 3. | At the end of that (at Join state 2), switch to either the Fast or Slow swim animation loop |
The fish can then remain in this loop until some other animation is required. To switch from Fast to Slow swim requires the current animation to be allowed to run until “Join State 2”, then the animation immediately switched, without any connecting animation.
The Animation Scheduler
Now the scheme above does not allow the AI to achieve instant responses to situations. It the case above, it needs to initiate a sequence of the animation steps to reach the turn animation. This needs each fish to potentially hold three animation states:
| Current | This is the current animation, which may either loop or be forced to finish | |
| Pending | This is the next animation to be triggered. By default this is “Null” | |
| Final | This is the final required animation, which also defaults to Null |
The current animation will be at some percentage stage of completion. If Pending is not Null, then the animations shuffle down, with Current set to Pending and Pending set to Final.
Linking the Animation to the AI
The scheme above will generally allow a relatively seamless transition between states, but is insensitive to events that require rapid response. If a fish is swimming towards a wall, the AI will need to anticipate the danger of collision and make some evasive moves. Fortunately walls are fairly predictable. A fish swimming towards the wall can predict when a collision will occur. This could be achieved using geometry, but is more simply handled by just calculating where the fish will be after time “n” and seeing if that results in collision.
Therefore a fish can afford to predict far in advance whether they will collide with the wall, so the AI has good advance notice of when the fish needs to switch from swim to turn.
However the collision object may be another fish. Now the task of avoiding collision is harder and needs a more sensitive system to allow a fish time to switch animations, as follows:
Dynamic Control of Animation
Although the fish animations are designed initially for fixed playback, the AI may require animation to be accelerated. Animation rate is already linked to speed, as a fish that starts swimming faster will need an accelerated animation. Add to this the animation scheduler needs to respond to critical requests by the AI. These are at various levels, such as “play out quickly” or “critical play out”. The scheduler then needs to determine where the sequence can be speeded up. For a start, the Drift animation loop can generally be abandoned at any stage, as it involves only minimal deformation during animation. The next level is to simply speed up existing animations. Of these the transition animations such as Swim to Drift can be accelerated very substantially without this causing an unrealistic animation effect. Collisions are more likely with fast moving fish, which might even have a complete animation skipped. Fortunately, if the motion is quick, the jump is too fast to be easily seen.
Adding Visual Variety to a Limited Set of Animations
The Aquarium is designed to be watched. If the animation control is limited, then this could quickly become unattractively repetitive. It is unsatisfying if it becomes obvious that a fish is clearly in one of either: drifting, swimming slowly or swimming fast states. This issue is addressed by the following:
| 1. | Varying the animation speed (as indicated above) | |
| 2. | Playing part animations | |
| 3. | Running extra animations in parallel |
(2) above is very useful and works by having the fish replace some drift time by partly animating shallow turns. This can be linked to very shallow turns by the fish, which may be essentially drifting but also slightly turning. For such a turn the Shallow Turn animation may proceed from 0% to 15%, and then reverse from 15% back down to 0%. The 15% limit depends on the fish speed. This adds some richness to the limited animation options.
(3) provides a substantial enhancement, which avoids the fish from repeating animation states, when drifting. This provides separate animation for the Pectoral fins and the eyes. Each of these can run randomised at different phases and speeds, resulting in the fish always being in a seemingly unique state during drifting. Drifting may sound dull, but fish do this a lot, and this is the state when you can most closely scrutinise the fish, so the need for variety is great. Note however that this direct control of Pectoral fin animation is turned off during swimming and turning, where this is best left to the model animator to match up the phasing of turning and fin behaviour.
Mapping a Single Animation to the Physics Control
The linking of an animation to the Physics Control might sound relatively trivial, but actually has substantial hidden complexity. A good example is the turn (in this case, the Sharp Turn below). During a turn the Physics Control needs to change the direction of the fish, but how is that done? If you examine the clips from a real Zebra Danio below:

From this you can see the Zebra during 4 phases, and it is clear that the centre of curvature moves along the body. The fish is actually moving snake-like through the water, with the body passing through a single turn point. The Zebra Danio was a fish that we had strong access to, so was a primary focus for analysis. However examining other fish suggested that this basic dynamic is common. Physically it makes sense, as any movement that requires significant displacement of the body either side of the fish’s position requires a lot of energy to displace water. The turn, in this case, is started by the head flexing.
What are the repercussions for the Physics Control? The Physics Control needs to determine when the fish switches direction and when it is moving and when not. If you simply “turn” the fish during the turn, keeping the speed constant, it looks terrible. In practice the fish has to actually stop moving forward, and this starts about 5% through the turn animation and then restarts at about 70%. The actual rotation of the fish finishes after about 60% of the turn. After this 60% turn finished, the fish actually gets faster, until the complete animation is finished.
This is a slight over-simplification, but shows that the mapping of the Physics Control to animation is critical.
Mapping the Fish Shape for Collisions
The previous section above Linking the Animation to the AI considered the problem of avoiding collisions. If this were Pool or Snooker, the issue of collisions is very simple. However a fish is a complex object. If collisions are mapped exactly to the model shape, then the processing cost of doing this is huge. This would pretty well eliminate the option of having the Physics Control predict collisions, as the Physics Control would not only need to know where each polygon is going to be after the fish moves, but also how the fish changes shape. This is out of the question.
An earlier article Optimised Navigation of Complex 3D Worlds showed the use of approximate bounding spheres to represent 3D models. This oversimplifies a model so that it can be easily manipulated. We could try mapping the whole fish with spheres, tailor made to each fish, resulting in a 3D structure of bounding spheres that would need to be rotated using matrix multiplication to determine how the array of spheres would move through space. Although simpler than using a whole model, this is complex and expensive for the Physics Control to project for collisions, and not practical.
The opposite extreme case is to consider using a single bounding sphere, as below (left):
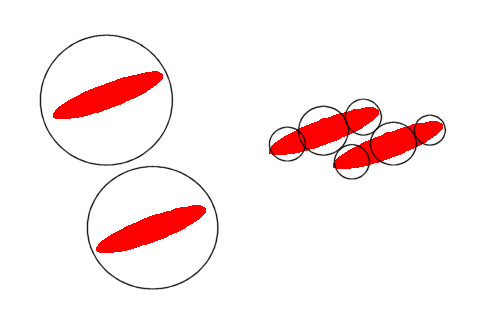
This has the problem, as can be seen above, that two fish could follow each other, but not swim past each other, as a single sphere takes no account of the fish shape. The compromise taken is to use 3 spheres to represent the fish (see right). Only two of these are mapped, and the third linear interpolated between these.
However this is still not quite enough. Consider the case of a Yellow Tang.
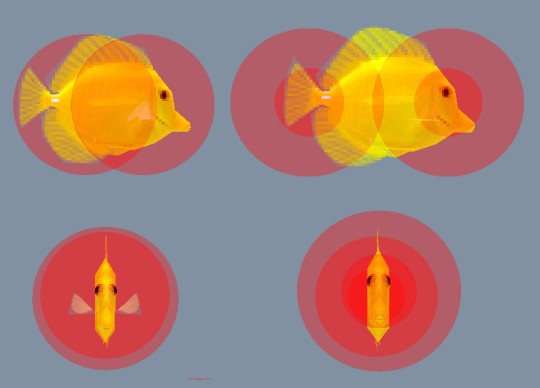
In this instance we have the basic two-sphere mapping on the left hand side (the 3rd linear interpolated sphere is not shown). These spheres need to be quite big to accommodate the full height of the Tang. This is a problem because, as can be seen from the picture bottom left, the Tang is then rather wide. In an AI emulation this means it cannot swim close to other fish or through narrow gaps. The consequence of this is greater than is immediately obvious. If you have a tank full of fishes with bloated bounding spheres, they quickly get in each other’s way and can easily cause traffic jams.
The solution is shown on the right hand side, where the Tang actually has 4 spheres, as two concentric pairs. These pairs get referenced in different situations. This requires the collision code to know the relative orientation of the Tang. If the fish is swimming horizontally, then the outer sphere is used to measure distance above and below the fish, and the inner sphere for positions next to and in front or behind the fish. If the fish tilts then the bounding sphere is interpolated between these, so that the effective sphere shrinks in size as the fish tilts down. This, for example, allows the fish to touch the bottom of the tank with its mouth.
Conclusions
The basic scheme above provides a relatively simple framework within which the fish Physics Control and AI can be implemented. The handling of animation is clearly separated from the Physics Control, but allows the Physics Control and AI to have some top-level control of how it is run. Finally the mapping of bounding spheres, with the interpolated inner and outer spheres, provides a system that is relatively fast to run. This gives the AI the freedom to test out strategies for movement, where a more costly system would not permit this.
The second part of this article will deal with the control of the AI. A further article will deal with how this product was developed using AI Factory’s generic testbed.
Jeff Rollason: February 2007
