Copyright Notice: All code and ideas expressed in this article, are Copyright AI Factory Ltd.
You may use these, only with the direct written permission of AI Factory Ltd.
Trying to sustain a viable framerate for an application on multiple instances of supported and limited hardware poses potential problems. Allowing the framerate to drop below 30 fps may result in an unacceptable jerky movement. However to handle the manipulation of multiple animated 3D objects requires a great deal of maths, needing multiple matrix operations to resolve the position of vertices. This requires careful management by the animation scheduler (thereafter here referred to as the "engine" or "animation engine"). An intelligent simulation might selectively swap models with simpler ones, when objects move away from near view, and optimise out others that may be obscured. These are relatively special tricks that depend on particular favourable conditions and may also have a memory hit. However if you want to sustain the framerate without dropouts, then a more universal technique needs to be used.
Cutting out the math
A significant cost is imposed by all the calculations on vertices required by animation. This might seem an inevitable evil, but actually there are options to help cut down the workload required.
If you consider the probable scenario of the difference between adjacent frames, then one fairly universal truth is that they will probably be very similar. Therefore one frame could be modified to generate the next frame. Our approach to this is to allow frame interpolation. This basic technique should be a very natural solution for baby-boomers, who were brought up on log tables that demanded the use of interpolation for every day maths. This now uncommon daily method is very useful in this context.
To give a simple example, imagine a single object animated in 3D space. If you are sustaining 30 fps, you could calculate every 8th frame and interpolate the rest. This requires a future projected state to be calculated and then used to generate interpolated frames from the current to this future state. The interpolated frames are much cheaper to calculate, simply requiring interpolation of each vertex between the end and start frame. In the image below, you can see the interpolation of a rotating square. Note that only the 4 vertices are interpolated. The actual square is generated from these modified vertices. This is not an ideal case to interpolate, but easily to diagrammatically show (see later).
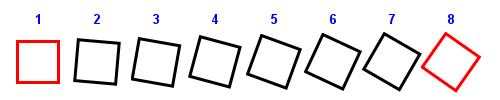
This looks promising, but you may have already appreciated that it still seems to leave 1 in every 8 frames as rather slow. If that was the case then we may even be worse off than before, with a flurry of fast frames followed by one slow one.
This is where intelligent scheduling comes in. If there was only one object, then likely as not, we could anyway probably render inside 30 fps. The gain comes from rendering multiple objects. Taking a simple instance, object A gets calculated for frame 1 and object B for frame 2, and so on. Now the expensive animation calculations are staggered, so that during any one frame only one object is being re-calculated, while the remainder are being interpolated, each at a different phase in the interpolation. The diagram below illustrates this.
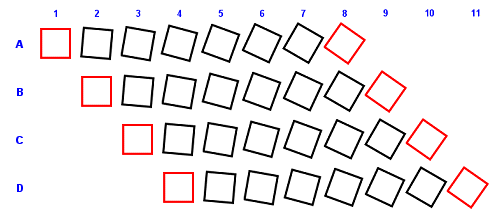
Interpolation Side effects
Of course this is highly specific in its handling. It would seem flawed if many objects were being rendered as 60 objects would impose a 2 second interval at 30 fps between re-calculated vertices. This brings out an obvious flaw in how it might look. Imagine the interpolation of an aeroplane flying below:
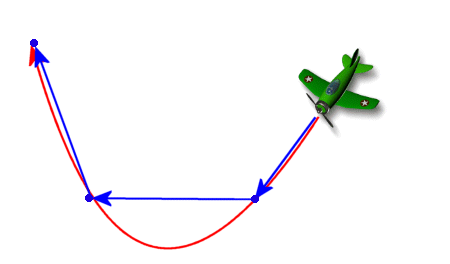
Clearly the plane may be sweeping in a curved flight, but this is replaced by a sequence of straight paths, making the flight artificially jerky and rather unreal. This highlights an intrinsic flaw with interpolation, in that it is only a substitute approximation, and can look bad. Of course the actual implementation should be more intelligent than this. The obvious thing to do is to calculate as much as you can within one frame. So that the engine calculates for as many objects as it can within one frame, leaving enough time to interpolate the rest. This will result in each frame calculating a group of objects at once, until time is running out and it switches to interpolation. Now maybe objects go through in groups of 4 at a time. Taking this further the objects could be of variable complexity, so that one frame may have 5 objects, and the next 8. Taking this further still the management could select objects to exactly fill the time slot, so maybe 3 complex objects plus a few tiny top-up objects. The diagram shows how this might work, showing staggered groups of object calculations.
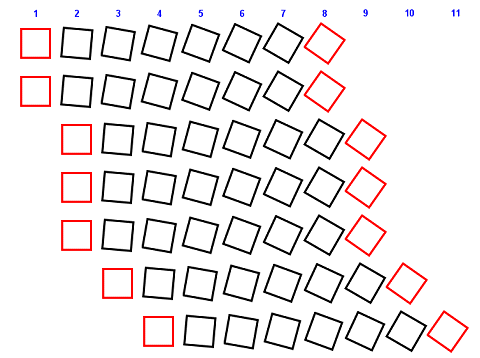
Note that this could give a variable interpolation interval. Note also that the engine needs to predict when an interpolation sequence will end. This could go wrong. If the interpolation sequence is too short, before the object location can be re-calculated, then the reference future interpolation point would be reached too early, and the engine would have to re-schedule an early re-calculation of a future reference point. This might be a problem if the error is repeated in multiple instances in the object list, as the scheduled recalculation may run the engine further short of time as other required calculations have to be deferred, resulting in the collapse of the framerate.
Of course that should not be allowed to happen, as the engine should dynamically adjust as it monitors the load, so that any local scheduling problem results in an instant adjustment to avoid the same thing happening again.
Additionally it would be helpful if the animation engine knew what was coming. Ideally the game engine would pre-warn the animation engine of some coming high cost animation event, so that the animation engine could adjust the scheduling to accommodate this.
Timing problems
This leads on to one obvious problem, that in order to interpolate animation, the engine needs to predict future positions of the object, which inevitably means that the game is vulnerable to lag. A user responding to an event may find that the system is sluggish to respond, as the current objects continue to be interpolated from an earlier future prediction. In practice a user intervention might attack some object, but that object is projected for a future where it is un-attacked.
The phenomenon will be familiar to those who have played on-line games such as Quake 3. These games need to allow for a built in lag, where a player may move to X, but actually moved to Y. The consequence is that a player may think they have grabbed some object, but actually that object has gone, but that event has not yet been logged. Quake 3 is good example of such a system that really performs pretty well, giving the user the illusion of a well synchronised system that seems to be responding quickly, even if lagged by half a second. In the instance of Quake, when a game projection is wrong, the player expected at position X may suddenly vanish, if they were actually somewhere else.
In this instance the performance of the target system will dictate the level of lag that will have to be used for interpolation. How you deal with that depends on the nature of the target game. You may be able to make intelligent projections to avoid mismatch, or even force projections to be acted out regardless.
Animations that may not interpolate well
Doing a linear projection of an animation may result in bad effects. To take an obvious example, a rapidly rotating object will interpolate badly. Consider a simple square that has been rotated through 180 degrees. The interpolation of this will result in the square apparently shrinking to a single point and then growing again to the final state. This is severe distortion. Even if only rotating through a smaller angle, the square will apparently shrink a little.

However an object moving in a straight line at a uniform speed from A to B will interpolate perfectly. If slightly curving, then the distortion will not be severe. If moving and slightly rotating, then this offers 2 distortions, both in position and size, but in practice the complex combination of movement and rotation will tend to mask the distortion, particularly if the object is moving rapidly.
Locked animations
Although this is very complex to manage, it is possible that objects might be broken into more than one model, so that one part might be animated with long periods of interpolation, while a second part with a complex animation is locked to shorter interpolation, or even no interpolation. This requires careful management, otherwise the interpolation may apparently break an object up, as the longer interpolation takes a different direct path between calculated points.
Conclusion
Interpolating animations provides a way for maintaining high framerates that otherwise could not be sustained on the target platform. If well managed it provides an application that can seamlessly provide a locked uniform high framerate on whatever target system. The cost is slight loss of animation accuracy and a potential lag problem. In general this is outweighed by the advantage of having continuous smooth animation, where a jerky slower framerate might ruin the quality of the game experience.
Of course this does not overcome other potential bottlenecks, such as simple rendering times. This may require careful management of texture sizes and ordering, to avoid unnecessary texture cache flushes. Rendering many textures over a large part of the screen may also overload the hardware's ability to render at that rate. However animation interpolation will probably make a big impact, reducing potential cpu bottlenecks.
Jeff Rollason and Dan Orme: September 2006
